Linear Algebra & Math

Matrices and Transforms

Transformation Matrix

The transform, rotation, and scale of an object can be represented with a 3x3 matrix. A identity matrix represents an object with no transforms, rotations, and with a scale of 1 1 1.

$identity=\left|\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right|$

Then, you apply the matrix by multiplying it with the current position to perform the transformation

matrix3 m = ident();
 
vector axis = {0,1,0};  //vector to rotate around
float angle = ch('angle'); //angle to rotate in radians
 
rotate(m,angle,axis);
@P *= m; 
 
//-----------------------------------------------------------
//You can also create a translation and rotation matrix
scale(m,{2,2,2,}); //scales the matrix by 2 in all axes
translate(m,{1,2,0}); //translates the matrix 1 unit in x and 2 units in y

Creating a Transform Matrix given 3 vector axes

Rotation Matrix from Axis Vectors

Listening to : The Decemberists (various) This is an oldie but a goodie, and I haven’t posted it anywhere else, so here it is before I forge.
https://renderdan.blogspot.com/2006/05/rotation-matrix-from-axis-vectors.html

vector x = {1,0,0};
vector y = {0,1,0};
vector z = {0,0,1};
//normalized vectors
 
4@xform = 
	set( x[0], x[1], x[2], 0,
	     y[0], y[1], y[2], 0,
	     z[0], z[1], z[2], 0,
	     0 , 0 , 0 , 1);

Tip

The code above generates a identity matrix, which is a matrix with 1s along the diagonal. This matrix represents a lack of any transformation. You can use the built in ident() function to generate a identity matrix of any size.

Vectors & Quaternions

Finding Angle between 2 Vectors

$\Theta =\arccos \frac{a\cdot b}{|a||b|}$

The angle between any two vectors is given by the formula above, where a is vector 1 and b is vector 2. The following is an implementation of the formula in Vex

vector v1 = {0,1,0};
vector v2 = {1,0,0};
 
 
f@theta = acos(
    (dot(v1,v2))/ 
    (v1 * v2) 
    );

Find Normal vector of plane given 3 points (A,B,C)

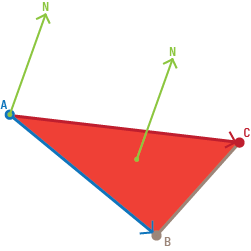
Both N vectors are equal

$\vec{N}=normalize((B-A)\times (C-A))$

Dot Product

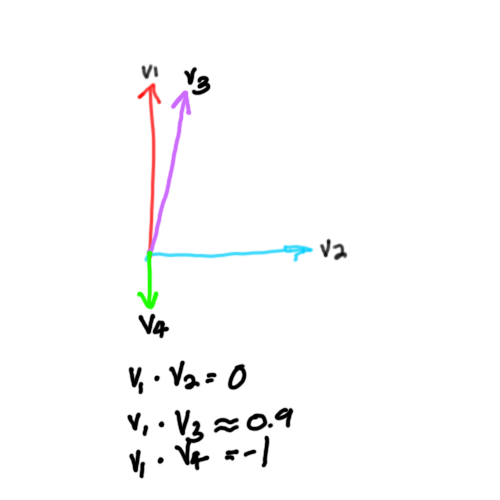
nice drawing

$vector1\ast vector2=scalar$

A dot product outputs a scalar value (from -1 to 1) that represents how similar the direction of 2 (normalized) vectors are.

If v1 is facing the same direction as v2, the dot product is 1

If v1 is facing the opposite direction as v2, the dot product is -1

If v1 is perpendicular to v2, the dot product is 0

This is useful for masking faces that face a certain direction, eg: masking all faces that face up for a snow accumulation effect.

vector v1 = {1,0,0};
vector v2 = {0,1,0};
//normalize the vectors or the float output will be out of range
f@dp = dot(v1,v2);

The Dreaded Quaternions

Quaternions are 4-dimensional vectors that define a rotation ( orientation ) in space. In Houdini you can easily manipulate quaternions using the built-in vex functions. (And you don’t have to do the math)

Quaternion rotation is preferred over Euler rotations as it does not suffer from gimbal lock, which is the loss of freedom in one axis after performing Euler rotations.

You can use quaternions to specify the rotation of points to be instanced onto, using the @orient attribute. The quaternion() function also readily converts a transformation matrix into a quaternion.

//------------Creating a quaternion from a matrix3
matrix3 m = ident();
vector axis = {1,0,0};  //vector to rotate around
float angle = ch('angle'); //angle to rotate in radians
//same as above
 
vector4 orient = quaternion(m); //create quaternion from matrix
 
p@orient = orient; //if you are instancing objects onto points with rotation
 
//------------Some Useful Quaternion Functions---------------
qrotate(orient,{0,1,0}); //rotates {0,1,0} by the given quaternion
qmultiply(q1,q2); //multiplies two quaternions
 
vector4 dihedral(v1,v2); //takes two vectors and computes the quaternion 
matrix3 dihedral(v1,v2); //or matrix that rotates v1 onto v2
 
slerp(q1,q2,weight); //Interpolates between two quaternions using weight attribute
 
qconvert(q1); //converts quaternion to a matrix3
quaterniontoeuler(q1); //converts a quaternion to an euler vector

There are a few other functions in vex related to manipulating quaternions that you can refer to here. The ones that I’ve listed above are just the most commonly used operations.

Kinematic Equation

$\hat{p}=p+vt+\frac{1}{2}a{t}^2$

p-hat = Displaced position
p = Initial Position v = Velocity t = Time a = Acceleration

You can use the kinematic equation to fairly accurately interpolate positions of fast moving geometry for accurate sourcing in simulations without using substeps. Another common usage of this equation is for acceleration based motion blur, which resolves curved motion blur better than velocity based motion blur.

Others

Choose Function

$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$

The choose function represents how many permutations there are in choosing k items from a set with a total number of n items.

For example, 9 choose 2 would result in 36, meaning there are 36 unique pairs of items within the set.

Principal Component Analysis

Principal component analysis (PCA) is a technique to reduce the dimensionality of data. PCA Shenanigans and How to ML | Jakob Ringler

Metric Tensors

Article by Jake Rice